Alligator Eggs!
A puzzle game by Bret Victor / May 1, 2007

Materials
Step 1: Print out this PDF onto six or so
different
colored
sheets
of
paper.
(Even better, photocopy it onto cardstock.)

Step 2: Print out this PDF onto a couple white sheets of paper.

Step 3: Cut out the pieces!

Pieces
These are hungry alligators:

Hungry alligators are hungry. They'll eat anything that's in front of them! But they are also responsible alligators, so they guard their families.
These are old alligators:

Old alligators are not hungry. They've eaten enough. All they do is guard their families.
These are eggs:
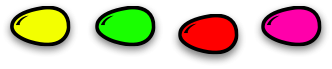
Eggs hatch into new families of alligators!
Families
Here's a small family:
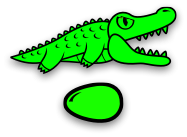
A green alligator is guarding her green egg.
Here's a slightly bigger family:
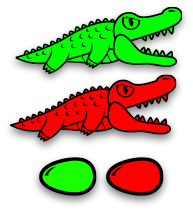
A green alligator and red alligator are guarding a green egg and a red egg. Or, you could say that the green alligator is guarding the red alligator, and the red alligator is guarding the eggs.
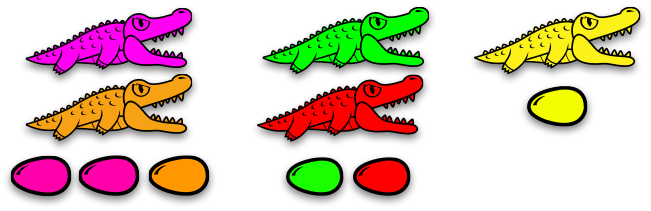
Here's a huge family!
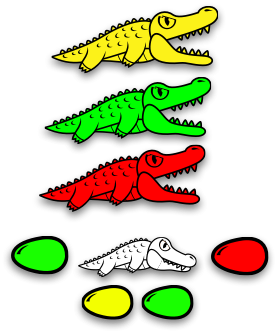
We've got yellow, green, red alligators guarding this family. They are guarding three things: a green egg, an old alligator, and a red egg. The old alligator is guarding a yellow egg and a green egg.
Notice that eggs only use the colors of the alligators guarding them. You can't have a blue egg without there being a blue alligator around to guard it.
Eating
Now, things are going to get messy. Here are two families, side-by-side:
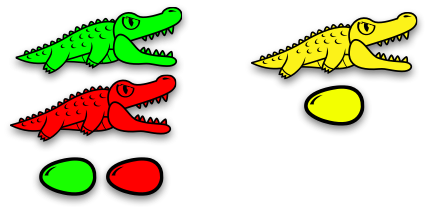
That green alligator sure is hungry. And there's a yellow family, right in front of her mouth, and it looks tasty!

I think you know what happens next.

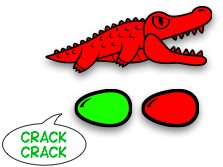
Unfortunately, the green alligator's eyes were bigger than her stomach. She ate too much!

And so she dies, and goes off to alligator heaven. But, the story doesn't end there. Because the green alligator died, the green egg starts to hatch...
Amazingly, it hatches into exactly what the green alligator ate. It's the miracle of life!
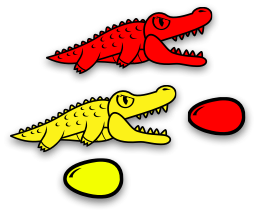
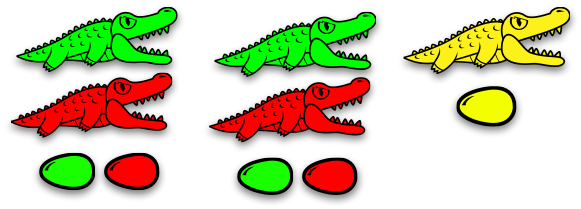
Now, we're down to one family. We have a red alligator guarding a yellow alligator and a red egg, and the yellow alligator is guarding her yellow egg.
But that yellow alligator sure is hungry, and there's a tasty red egg in front of her. Here we go again...

Poor alligator. Even a single egg is too much for her stomach!

The yellow alligator dies... but once again, the yellow egg starts to hatch...

And it hatches into exactly what the yellow alligator ate!
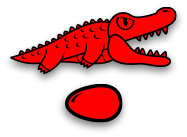
Now, there's nothing for anyone to eat, so we stop.
The Eating Rule
That was an example of the first rule of the game: the eating rule.
The eating rule says that if there are some families side-by-side...
the top-left alligator eats the family to her right.

Then, that alligator dies. But if she was guarding any eggs of the same color, each of those eggs hatches into what she ate.

The Color Rule
Continuing with the example above, the orange alligator eats the yellow family, leaving this:
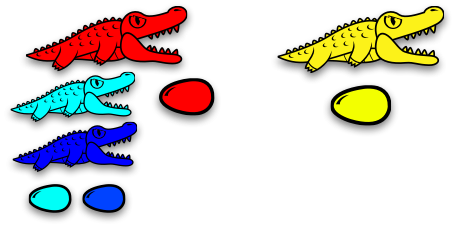
Now, the green alligator at the top-left wants to eat the family to her right. But before she can do so, we need to look at the color rule.
The color rule says that if an alligator is about to eat a family, and there's a color that appears in both families, we need to change that color in one family to something else.
In the picture above, green and red appear in both the first and second families. So, in the second family, we switch all of the greens to cyan, and all of the reds to blue.

Now that they don't share any colors, we can eat!
And eat!

And eat!

And eat, until there's nothing more that can be eaten.
Old Alligators
There's only one more rule in this game, and it has to do with old alligators:
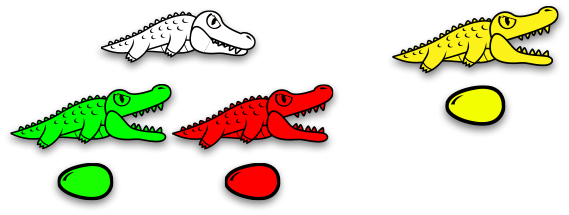
The top-left alligator here is not hungry. She's not going to eat anything. All she cares about is her family. So, how does she die?
She dies when she's only guarding one thing. Right now, she's guarding both a green family and a red family. They need her to take care of them. But that green alligator is hungry. The green alligator eats the red family...

Now, the old alligator is only guarding a single family. That family can take care of itself. She's no longer needed. So, she grows old and dies.

That is the old age rule. When an old alligator is just guarding a single thing, it dies.

Now, the red alligator eats the yellow family, and there's no more that can be eaten.
Gameplay
The game would consist of a series of puzzles, challenging the player to devise a family that, when fed X, produces Y. For example:
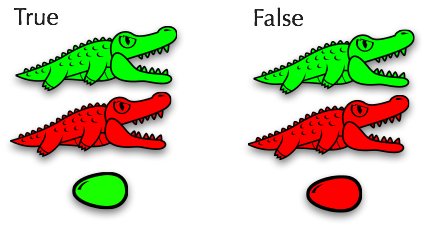
Here are two families. They are named "True" and "False":
And here is a family called "Not":
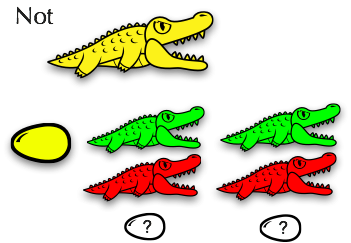
When "Not" eats "True", it produces "False". And when "Not" eats "False", it produces "True". What colors should the two eggs at the bottom be?
(For this to work well, we'd need a better color rule, to explain that families with different colors in the same "pattern" are equivalent.)
These puzzles could be embedded into a story. The player would have to solve each puzzle to see what happens next. Alternatively, this could be made into a board game. Each player would roll a die, travel forward a number of spaces, and solve the puzzle at the destination.
Theory
This game represents the untyped lambda calculus. A hungry alligator is a lambda abstraction, an old alligator is parentheses, and eggs are variables. The eating rule corresponds to beta-reduction. The color rule corresponds to (over-cautious) alpha-conversion. The old age rule says that if a pair of parentheses contains a single term, the parentheses can be removed.
Variations
Oliver Steele pointed out that family roles are very important to children, and more could be made of the concept of grandparent alligators, parents, babies (eggs), and so on. Currently, variable names are represented with colors. Both are arbitrary, and require renaming/recoloring rules to avoid capture. An alternative may be something like de Bruijn indices, corresponding to birth order and family relation.
Oliver also suggested that kids might not like the idea of parents dying, and perhaps alligator removal could be explained as moving away.
By changing the game so alligators are greedy, and eat everything to their right, we represent a right-associative lambda calculus. This seems to eliminate a lot of old alligators (parentheses) in Church numerals, the Y combinator, etc. Unfortunately, it means that old alligators have to be born when an alligator eats more than one thing, among other problems. I'd still like to figure out how to make Church numerals (repeated application) look less ugly.
Schematic Form
I've found that a schematic form of alligator calculus is actually rather handy for calculating lambda terms by hand. We draw a lambda as a line with a mouth. Parentheses are a line without a mouth. Here's the identity function:

Here are some Church numerals:
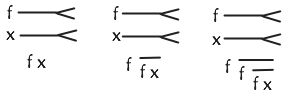
Here are boolean AND and OR (assuming the standard definitions for TRUE and FALSE):
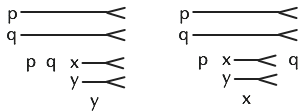
The Y combinator:
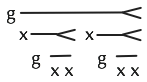
I don't know if these are any easier to read than the standard notation, but I've found them to be easier to work with, using pencil and paper. I imagine the terms eating one another and hatching below. I don't get lost in a long chain of symbols, losing track of what's applying to what.